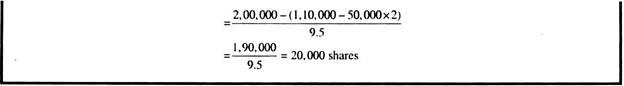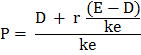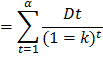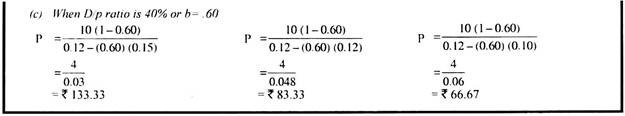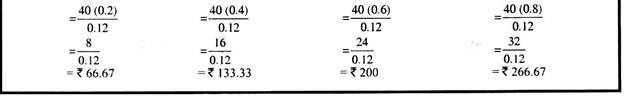This article throws light upon the two main concepts of dividend. The concepts are: 1. The Irrelevance Concept of Dividend 2. The Relevance Concept of Dividend.
Concept # 1. The Irrelevance Concept of Dividend:
A. Residual Approach:
According to this theory, dividend decision has no effect on the wealth of the shareholders or the prices of the shares, and hence it is irrelevant so far as the valuation of the firm is concerned. This theory regards dividend decision merely as a part of financing decision because the earnings available may be retained in the business for re-investment.
But, if the funds are not required in the business they may be distributed as dividends.
Thus, the decision to pay dividends or retain the earnings may be taken as a residual decision. This theory assumes that investors do not differentiate between dividends and retentions by the firm. Their basic desire is to earn higher Return on their investment.
In case the firm has profitable investment opportunities giving a higher rate of return than the cost of retained earnings, the investors would be content with the firm retaining the earnings to finance the same.
However, if the firm if not in a position to find profitable investment opportunities, the investors would prefer to receive the earnings in the form of dividends. Thus, a firm should retain the earnings if it has profitable investment opportunities otherwise it should pay them as dividends.
B. Modigliani and Miller Approach (Mm Model):
Modigliani and Miller have expressed in the most comprehensive manner in support of the theory of irrelevance. They maintain that dividend policy has no effect on the market price of the shares and the value of the firm is determined by the earning capacity of the firm or its investment policy.
The splitting of earnings between retentions and dividends, may be in any manner the firm likes, does not affect the value of the firm. As observed by M.M. “Under conditions of perfect capital markets, rational investors, absence of tax discrimination between dividend income and capital appreciation, given the firm’s investment policy, its dividend policy may have no influence on the market price of the shares. ”
Assumptions of MM Hypothesis:
The MM hypothesis of irrelevance of dividends is based on the following assumptions:
(i) There are perfect capital markets.
(ii) Investors behave rationally.
(iii) Information about the company available to all without any cost.
(iv) There are no floatation and transaction costs.
(v) No investor is large enough to effect the market price of shares.
(vi) There are either no taxes or there are no differences in the tax rates applicable to dividends and capital gains.
(vii) The firm has a rigid investment policy.
(viii) There is no risk or uncertainty in regard to the future of the firm. (MM dropped this assumption later).
The Argument of MM:
The argument given by MM in support of their hypothesis is that whatever increase in the value of the firm results from the payment of dividend, will be exactly off set by the decline in the market pride of shares because of external financing and there will be no change in the total wealth of the shareholders.
For example, if a company, having investment opportunities, distributes all its earnings among the shareholders, it will have to raise additional funds from external sources. This will result in the increase in number of shares or payment of interest charges, resulting in fall in the earnings per share in the future.
Thus whatever a shareholder gains on account of dividend payment is neutralised completely by the fall in the market price of shares due to decline in expected future earnings per share. To be more specific, the market price of a share in the beginning of a period is equal to the present value of dividends paid at the end of the period plus the market price of the shares at the end of the period.
This can be put in the form of the following formula:
P0 = D1 + P1/1+Ke
Where P0 = Market price per share at the beginning of the period, or prevailing market price of a share
D1 = Dividend to be received at the end of the period.
P1 = Market price per share at the end of the period.
Ke = Cost of equity capital or rate of capitalisation.
The value of P1 can be derived by the above equation as under:
P1= P0 (1+ke) – D1
The MM hypothesis can be explained in another form also presuming that investment required by the firm on account of payment of dividends is financed out of the new issue of equity shares.
In such a case, the number of shares to be issued can be computed with the help of the following equation:
m = I (E-nD1)/P1
Further, the value of the firm can be ascertained with the help of the following formula:
nP0 (n + m) P1 – (I-E)/1 + ke
Where, m = number of shares to be issued.
I = Investment required.
E = Total earnings of the firm during the period,
P1 = Market price per share at the end of the period.
Ke = Cost of equity capital.
n = number of shares outstanding at the beginning of the period.
D1 = Dividend to be paid at the end of the period.
np0 = Value of the firm
Let us take the following illustration to illustrate MM hypothesis of irrelevance of dividend to the valuation of firm:
Illustration 1:
ABC Ltd. belongs to a risk class for which the appropriate capitalisation rate is 10%. It currently has outstanding 5,000 shares selling at Rs. 100 each. The firm is contemplating the declaration of dividend of per share at the end of the current financial year.
The company expects to have a net income of Rs. 50,000 and has a proposal for making new investments of Rs 1,00,000. Show that under the MM hypothesis, the payment of dividend does not effect the value of the firm.
Solution:
Illustration 2:
Expandent Ltd. had 50,000 equity shares of Rs. 10 each outstanding on January 1. The shares are currently being quoted at par in the market. In the wake of the removal of dividend restraint, the company now intends to pay a dividend of Rs. 2 per share for the current calendar year. It belongs to a risk- class whose appropriate capitalisation rate is 15%.
Using MM model and assuming no taxes, ascertain the price of the company’s share as it is likely to prevail at the end of the year (i) when dividend is declared, and (ii) when no dividend is declared. Also find out the number of new equity shares that the company must issue to meet its investment needs of Rs. 2 lakhs, assuming a net income of Rs. 1.1 lakhs and also assuming that the dividend is paid.
Solution:
Criticism of MM Approach:
MM hypothesis has been criticised on account of various unrealistic assumptions as given below:
1. Prefect capital market does not exist in reality
2. Information about the company is not available to all the persons.
3. The firms have to incur flotation costs while issuing securities.
4. Taxes do exit and there is normally different tax treatment for dividends and capital gains.
5. The firms do not follow a rigid investment policy.
6. The investors have to pay brokerage, fees, etc. while doing any transaction.
7. Shareholders may prefer current income as compared to further gains.
Concept # 2. The Relevance Concept of Dividend:
The other school of thought on dividend decision holds that the dividend decisions considerably affect the value of the firm. The advocates of this school of thought include Myron Gordon, Jone Linter, James Walter and Richardson.
According to them dividends communicate information to the investors about the firms’ profitability and hence dividend decision becomes relevant. Those firms which pay higher dividends will have greater value as compared to those which do not pay dividends or have a lower dividend payout ratio.
We have examined below two theories representing this notion:
A. Walter’s Approach, and
B. Gordon’s Approach
A. Walter’s Approach:
Prof. Walter’s approach supports the doctrine that dividend decisions are relevant and affect the value of the firm. The relationship between the internal rate of return earned by the firm and its cost of capital is very significant in determining the dividend policy to subserve the ultimate goal of maximising the wealth of the shareholders.
Prof. Walter’s model is based on the relationship between the firm’s:
(i) Return on investment, i.e. r, and
(ii) The cost of capital or the required rate of return, i.e., k.
According to Prof. Walter, If r > k i.e., if the firm earns a higher rate of return on its investment than the required rate of return, the firm should retain the earnings. Such firms are termed as growth firms and the optimum pay-out would be zero in their case. This would maximise the value of shares.
In case of declining firms which do not have profitable investments, i.e., where r < k, the shareholders would stand to gain if the firm distributes its earnings. For such firms, the optimum pay-out would be 100% and the firms should distribute the entire earnings as dividends.
In case of normal firms where r = k, the dividend policy will not affect the market value of shares as the shareholders will get the same return from the firm as expected by them. For such firms, there is no optimum dividend payout and the value of the firm would not change with the change in dividend rate.
Assumption of Walter’s Model:
(i) The investments of the firm are financed through retained earnings only and the firm does not use external sources of funds.
(ii) The internal rate of return (r) and the cost of capital (k) of the firm are constant.
(iii) Earnings and dividends do not change while determining the value.
(iv) The firm has a very long life.
Walter‘s Formula for Determining the Value of a Share:
Walter has developed a mathematical equation to ascertain the market price of a share which enables a firm to arrive at the appropriate dividend decision.
His equation is based on the following share valuation model:
P = D/ke-g
Where, P = Price of equity share
D = Initial dividend per share
ke = Cost of equity capital
g = Expected growth rate of earnings/dividend
Prof. Walter has given the following formula to ascertain the market price of a share:
or
where, P = Market price per share
D = Dividend per share
r = Internal rate of return
E = Earnings per share
ke = Cost of equity capital
Let us take the following illustration to understand the above equation.
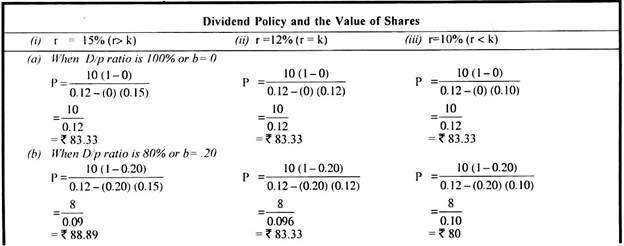
Illustration 3:
The following information is available in respect of a firm.
Capitalisation rate = 10%
Earnings per share = Rs. 50
Assumed rate of return on investments:
(i) 12%
(ii) 8%
(iii) 10%
Show the effect of dividend policy on market price of shares applying Walter’s formula when dividend payout ratio is (a) 0% (b) 20%, (c) 40%, (d) 80%, and (e) 100%
Solution:
Conclusion:
From the above analysis we can draw the conclusion that when,
(i) r>k, the company should retain the profits, i.e., when r=12%. ke=10%;
(ii) r is 8%, i.e., r<k, the pay-out should be high; and
(iii) r is 10%; i.e., r=k; the dividend pay-out does not affect the price of the share.
Criticism of Walter’s Model:
Walter’s model has been criticised on account of various assumptions made by Prof. Walter in formulating his hypothesis:
(i) The basic assumption that investments are financed through retained earnings only is seldom true in real world. Firms do raise funds by external financing.
(ii) The internal rate of return, i.e., r, also does not, remain constant. As a matter of fact, with increased investment the rate of return also changes.
(iii) The assumption that cost of capital (k) will remain constant also does not hold good. As a firm’s risk pattern does not remain constant, it is not proper to assume that k will always remain constant.
B. Gordon’s Approach:
Myron Gordon has also developed a model on the lines of Prof. Walter suggesting that dividends are relevant and the dividend decision of the firm affects its value.
His basic valuation model is based on the following assumptions:
(i) The firm is an all equity firm.
(ii) No external financing is available or used. Retained earnings represent the only source of financing investment programmes.
(iii) The rate of return on the firm’s investment r is constant.
(iv) The retention ratio, b, once decided upon is constant. Thus, the growth rate of the firm g = br, is also constant.
(v) The cost of capital for the firm remains constant and it is greater than the growth rate, i.e. k > br.
(vi) The firm has perpetual life.
(vii) Corporate taxes do not exist.
According to Gordon, the market value of a share is equal to the present value of future stream of dividends.
Thus,
Gordon’s basic valuation formula can be simplified as under:
or,
where, P = Price of shares
E = Earnings per share
b = Retention ratio
ke = Cost of equity capital
br =g=Growth rate in r,i.e., rate of return on investment of an all-equity firm
D0 = Dividend per share
D1 = Expected dividend at the end of year 1.
The implications of Gordon’s basic valuation model may be summarised as below:
1. When the rate of return of firm on its investment is greater than the required rate of return, i.e., when r > k, the price per share increases as the dividend payout ratio decreases. Thus, growth firm should distribute smaller dividends and should retain maximum earnings.
2. When the rate of return is equal to the required rate of return, i.e., when r = k, the price per share remains unchanged and is not affected by dividend policy. Thus, for a normal firm there is no optimum dividend payout.
3. When the rate of return is less than the required rate of return, i.e., when r < k, the price per share increases as the dividend payout ratio increases. Thus, the shareholders of declining firm stand to gain if the firm distributes its earnings. For such firms, the optimum pay out would be 100%.
Illustration 4:
The following information is available in respect of the rate of return on investment (r), the cost of capital (k) and earning per share (E) of ABC Ltd.
Rate of return on investment (r) = (i) 15%; (ii) 12%; and (iii) 10%
Cost of capital = (k) 12%
Earning per share (E) = Rs. 10
Determine the value of its shares using Gordon’s Model assuming the following:
Solution:
Gordon’s Revised Model:
The basic assumption in Gordon’s Basic Valuation Model that cost of capital (k) remains constant for a firm is not true in practice. Thus, Gordon revised his basic model to consider risk and uncertainty. In the revised model, he suggested that even when r = k, dividend policy affects the value of shares on account of uncertainty of future, shareholders discount future dividends at a higher rate than they discount near dividends.
That is there is a two fold assumption, viz.:
(i) investors are risk averse, and
(ii) They put a premium on a certain return and discount/penalise uncertain returns.
Because the investors are rational and they want to avoid risk, they prefer near dividends than future dividends. This argument is described as bird-in-the hand argument, i.e. the value of a rupee of dividend income is more than the value of rupee of capital gain.
In the words of Krishnan, John, E. “of two stocks with identical earnings, record, prospects, but the one paying a larger dividend than the other, the former will undoubtedly command a higher price merely because shareholders prefer present to future values. Mypic vision plays part in the price-making process. Stockholders often act on the principle that a bird in hand is worth than two in the bushes and for this reason are willing to pay a premium for the stock with the higher dividend rate, just as they discount the one with the lower rate.”
Thus, if dividend policy is considered in the context of uncertainty, the cost of capital cannot be assumed to be constant and so firm should set a high dividend payout ratio and offer a high dividend yield in order to minimise its cost of capital.
Illustration 5:
The following information is available in respect of return on investment (r), the cost of capital (ke) and earning per share (E) of XYZ Ltd.
r = 10 percent
E =Rs. 40
Determine the value of its shares using Gordon’s Model, assuming the following:
Solution:
Illustration 6:
A company is expected to pay a dividend of Rs. 6 per share next year. The dividends are expected to grow perpetually at a rate of 9 per cent. What is the value of its share if the required rate of return is 15%?
Solution:
Illustration 7:
The current price of a company’s share is Rs. 75 and dividend per share is Rs. 5. Calculate the dividend growth rate, if its capitalisation rate is 12 percent.
Solution:
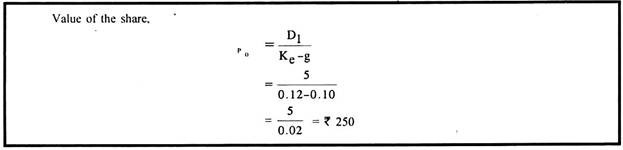
Illustration 8:
The current price of a company’s share is Rs. 200. The company is expected to pay a dividend of Rs. 5 per share next year with an annual growth rate of 10 per cent. If an investor’s required rate of return is 12%, should he buy the share?
Solution:
As the value of the share (Rs. 250) is more than its current price of Rs. 200, the investor should buy the share.
Illustration 9:
The book value per share of a company is Rs. 145.50 and its rate of return on equity is 10 percent. The company follows a dividend policy of 60% pay out. What is the price of its share if the capitalisation rate is 12 percent?
Solution:
Illustration 10:
A company decides that it will not pay any dividends for 20 years. After that time it is expected that the company could pay dividend of Rs. 15 per share indefinitely. However, the company at present could pay Rs. 3 per share. The required rate of this company’s shareholders is 10 percent. What is the loss to each shareholder as a result of the policy of the company?
Calculate the value of the equity share:
Solution:
Illustration 11:
A large sized chemical company has been expected to grow at 14% per year for the next 4 years and then to grow indefinitely at the same rate as the national economy, i.e. 5%. The required rate of return on the equity shares is 12% Assume that the company paid a dividend of Rs. 2 per share last year (D0 = 2). Determine the market price of the shares today.
You may use the following table:
Solution:
Illustration 12:
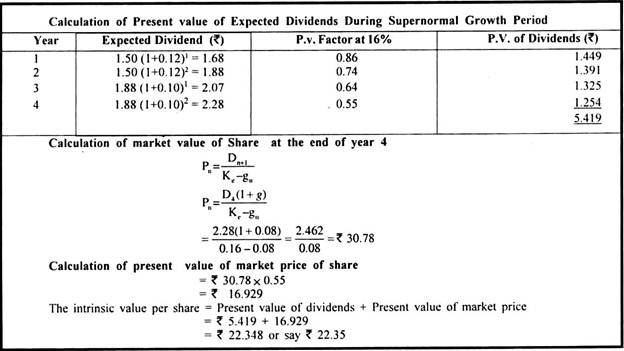
X Ltd. is foreseeing a growth rate of 12% per annum in the next 2 years. The growth rate is likely to fall to 10% for the third and fourth year. After that the growth rate is expected to stabilise at 8% per annum. If the last dividend paid was Rs. 1.50 per share and the investor’s required rate of return is 16%, find out the intrinsic value per share of X Ltd. as of date.
You may use the following table:
Solution: