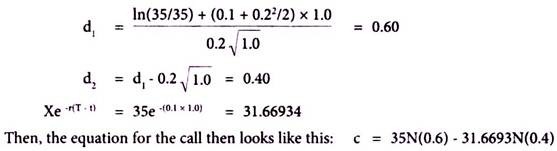Prof. Robert C. Metron and Prof. Myron S. Scholes have been awarded Nobel prize in Economics in 1997 for having developed a pioneering formula for the valuation of derivatives and other stock options. In fact, they developed this method in collaboration with Prof. Fischer Black, who died in 1995.
In 1973 Black and Scholes published what has come to be known as the Black-Scholes formula. Prof Metron developed on this and devised another method to derive the formula that turned out to have wider applicability.
Nowadays, thousands of traders and investors use the formula every day to value of stock options in markets throughout the world. Black, Metron and Scholes made a vital contribution by showing that it is in fact not necessary to use any risk premium when valuing an option. This does not mean that the risk premium disappears, but that it is already rated in the stock price.
The Black-Scholes model for valuing a European call is:
C = SN (d1) – Xe-r(T-1)N(d2)
C= Call option premium
S = Current asset price
X = Exercise price
T-t = Time to expiry in decimals of a year
σ = The annualized standard deviation of the natural log of the asset price relativw in decimals
ln = Natural logarithm
N(d1) = Cumulative standard normal probability distribution.
d1 and d2 = Standardized normal variables
R = Risk-free rate of interest in decimals (continuously compounded)
Assumptions of Black-Scholes Model:
In deriving their option pricing model, which calculates the value of a call option, Black and Scholes made the following assumptions:
1. The stock underlying the call option pays no dividends during the life of the option.
2. There are no transaction costs in buying or selling either the stock or the option.
3. The short-term, risk free interest rate is known constant during the life of the option.
4. Any purchaser of a security may borrow any fraction of purchase price at the short-term, risk-free interest rate.
5. Short selling is permitted without penalty, and the short seller will receive immediately the full cash proceeds for a security sold short.
6. Trading in all securities take place in continuous time, and the stock price moves randomly in continuous time.
The Black Scholes formula is developed from the principle that options can completely eliminate market risk from a stock portfolio. Black and Scholes postulate that the ratio of options to stock in this hedged position is constantly modified as no commission cost in order to offset gains or losses on the stock by losses or gains on the options. Because the position is theoretically riskless, we would expect the hedge to earn the risk-free rate, somewhat analogous to the assumption invoked in deriving the capital asset pricing model (CAPM).
Given that the risk-free hedge should earn the risk-free rate, we infer that the option premium at which the hedge yields a return equal to the risk-free short-term interest rate is the fair value, the return from a risk-free hedged position could be different from the risk-free interest rate. Because this is inconsistent with equilibrium, we would expect the option price to adjust towards fair value.
Problem:
The current asset price is 35.0, the exercise price is 35.0, the risk-free rate of interest is 10%, the volatility is 20% and the time to expiry is one year. Thus S = 35, X = 35, (T -1) = 1.0, r = 0.1 and σ = 0.2.
Solution:
First, we calculate d1, then d2 and, finally, the present value of the exercise price Xe –r(T-t)
Solution:
Here, d1 is a standardized normal random variable N(d1) is a cumulative standardized normal probability distribution. It represents the area under the standardized normal curve from Z.
By referring to mathematical table given at the end of book on the standardized normal distribution we can arrive at the values of N(d1) and N(d2) as follows:
The value of N(d1) when d1 = 0.6 is 0.7257
The value of N(d2) when d2 = 0.4 is 0.6554
When the above values are substituted in the equation, then
c = 35 (0.7257) – 31.6693 (0.6554) = 4.6434