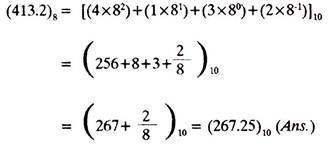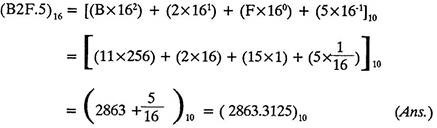This article throws light upon the four main types of number system. The types are: 1. Decimal System 2. Binary System 3. The Octal System 4. The Hexadecimal System.
Type # 1. Decimal System:
In decimal system the base (or radix) is 10, since any position can contain one of ten digits, refer (3) above. The system therefore has a carrying factor of 10 and each digit indicates a value which depends on the position it occupies, for example;
In 6421 the digit 6 signifies 6 x 1000
In 4621 the digit 6 signifies 6 x 100
ADVERTISEMENTS:
In 4261 the digit 6 signifies 6 x 10
and in 4216 the digit 6 signifies 6
The decimal system uses ten digits to record the number. The ten digits are 0, 1, 2, 3, 4, 5, 6, 7, 8 and 9 and any number (used) is based upon power of 10.
For example 5281 is made up of:
ADVERTISEMENTS:
(5 x 103) + (2 x 102) + (8 x 101) + (1 x 100)
= 5000 + 200 + 80 + 1 = 5281.
Type # 2. Binary System:
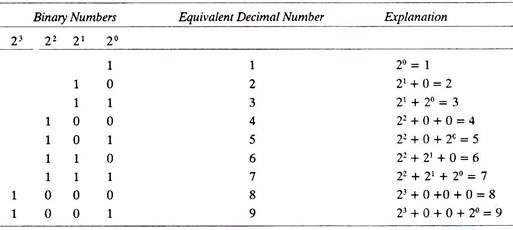
Whereas decimal system uses ten digits to record the number, the binary system uses only two digits (for recording the number) that is 0 and 1, and its base is 2 (whereas that of decimal system is 10). Although in everyday life, people generally use the decimal number system for counting, it is more convenient to use the binary number system in a computer because electronic components are usually in one of two states, which can be used to represent 0 and 1, the two digits used in the binary system.
To elaborate it further:
ADVERTISEMENTS:
The computer does not have a large number of symbols for representing data. It has only two, 0 and 1 (called binary digits or bits). These correspond to the two electronic or magnetic states used in computer circuits and storage.
For example if a punched paper tape is used in the computer, a hole in a tape may allow electrical contact to be made (ON) and the absence of a hole in the tape does not allow electrical contact to be made (OFF). Therefore a hole can represent 1 and no hole can represent 0. Binary system is more compact than the decimal system of coding as the latter will need large size of the storage medium and relative complexity of the reading device.
Given below is the table of construction of Binary numbers:
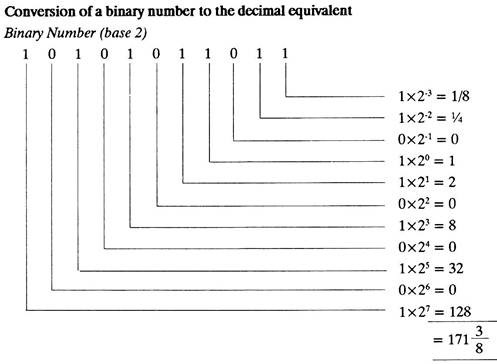
Conversion of a Decimal Number to Binary Equivalent:
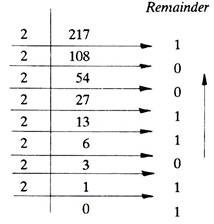
(a) Let the decimal number be 217.
To find the binary equivalent proceed as follows:
Start binary number with last digit. Therefore the binary equivalent of 217 is 11011001.
ADVERTISEMENTS:
(b) Convert .8125 into binary number.
(c) Convert decimal number 217.8125 into binary number
ADVERTISEMENTS:
From (a) and (b) above =
Type # 3. The Octal System:
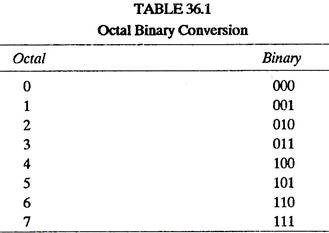
The octal system (base 8) and hexadecimal system (base 16) are of importance because they can be used as a shorthand for binary numbers. This is because three binary digits can be represented by the numbers 0 to 7 i.e., the octal range, while four binary digits can be represented by the numbers 0 to 9 and A to F.
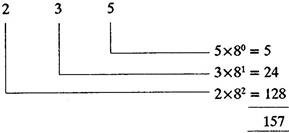
(a) Conversion of Octal number into Decimal equivalent
Let octal number be (235)8
Hence (235)8 = (157)10
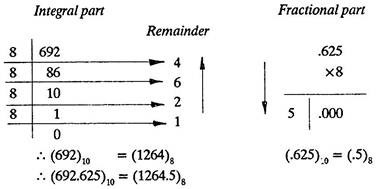
(b) Conversion of decimal number into octal equivalent
ADVERTISEMENTS:
Let the decimal number be 692.625
(c) Convert (413.2)8 into Decimal equivalent
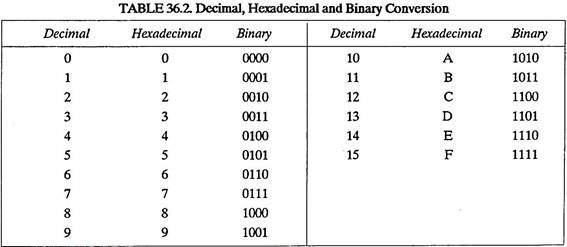
Type # 4. The Hexadecimal System:
The hexadecimal system has a base 16 and the digits 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 and letters A, B, C, D, E, F are used. The letters A, B, C, D, E and F represent the decimal numbers 10, 11, 12, 13, 14 and 15 respectively.
ADVERTISEMENTS:
(a) Conversion of decimal number (259.8125)10 into hexadecimal form
(b) Conversion of hexadecimal number B2F.5 into Decimal equivalent.
When hexadecimal is used to represent a binary number, the individual hexadecimal digits represent successive groups of four binary digits starting at the point. This is similar to the conversion from binary to octal, in which each set of three bits is translated to an octal digit.