The computer user does not usually need to be able to perform binary arithmetic, but some understanding of binary arithmetic is a useful background for understanding computers. Here, in this article, the rules for each of the four basic arithmetic operations of addition, subtraction, multiplication and division will be explained and illustrated for the binary system.
1. Binary Addition:
Rules for binary addition
1 + 1 = 0 and carry 1 to add to next column
1 + 0 = 1
0 + 1 = 1
0 + 0 = 0
2. Binary Subtraction:
Rules for binary subtraction
1 – 1 = 0
1 – 0 = 1
0 – 1 = 1 with a borrow from the next column of the minuend.
0 – 0 = 0
In subtraction, the borrow reduces the remaining minuend by 1. A borrow will cause a 1 in the next column to the left in the minuend to become 0. If the next column contains a 0, it is changed to a 1, and the succeeding 0s in the minuend are changed to is until a 1 can be changed to 0, for example:
* Carry changes 0 to 1
**Continue changing 0s to 1s
***Until a 1 can be changed to a 0 then proceed with subtraction.
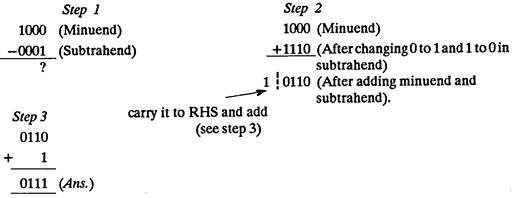
Binary subtraction can be carried out in another way also as explained below:
Taking the same problem as solved above.
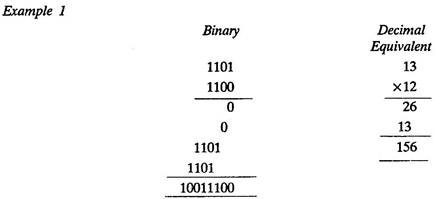
3. Binary Multiplication:
Rules for binary multiplication
Copy multiplicand when multiplier digit is 1; do not when it is 0.
Shift as in decimal multiplication.
Add the resulting binary numbers according to the binary addition.
Examples of binary multiplication.
4. Binary Division:
Rules for binary division:
a. Start from the left on the dividend.
b. Perform a series of subtractions in which the divisor is subtracted from the dividend.
c. If subtraction is possible, put a 1 in the quotient and subtract the divisor from the corresponding digits in the dividend.
d. If subtraction is not possible (divisor greater than remainder), record a 0 in the quotient.
e. Bring down the next digit to add to the remainder digits. Proceed as before in a manner similar to long division.
Proceed as before in a manner similar to long division.
Example: