In this article we will discuss about the return and risk on single asset.
Return on Single Asset:
The typical object of investment is to make current income from investments in the form of dividends and interest income. The investments should earn reasonable and expected rate of return on investments. Certain investments like bank deposits, public deposits, debentures, bonds etc. will carry a fixed rate of return payable periodically.
In case of investments in shares of companies, the periodical payments in the form of dividends are not assured, but it may ensure higher returns than fixed income investments. But the investments in equity shares of companies carry higher risk than fixed income instruments.
Another form of return is in the form of capital appreciation. This element of return is the difference between the purchase price and the price at which the asset can be sold, it can be a capital gain or capital loss arising due to change in the price of the investment.
The rate of return of a particular investment is calculated as follows:
Annual Rate of Return:
The annual rate of return of a particular investment can be calculated as follows:
Where, R = Annual rate of return of a share
D1 = Dividend paid at the end of the year
P0 = Market price of share at the beginning of the year
P1 = Market price of share at the end of the year
The above formula is used for calculation of annual return of an investment in shares. In the above formula, D1/P0 represents dividend yield and (P1 – P0)/P0 represents capital gain or loss.
Problem 1:
Mr. Ravi has purchased 100 shares of Rs.10 each of Radheshyam Ltd. in 2013 at Rs.78 per share. The company has declared a dividend @ 40% for the year 2015-16. The market price of share as at 1-4-2015 was Rs.104 and on 31-3-2016 was Rs.128. Calculate the annual return on the investment for the year 2015-16.
Solution:
Dividend received for 2015-16 = Rs.10 x 40/100 = Rs.4
Calculation of Annual Rate of Return on Investment for the Year 2015-16:
Average Rate of Return:
The rate of return can also be calculated for a period more than one year. The average rate of return represents the average of annual rates of return over a period of years.
The formula used for calculation of average rate of return is given below:
Where, R̅ = Average rate of return
R1, R2 …..Rn = Annual rate of return in period 1, 2,…..
n = Total number of periods
Problem 2:
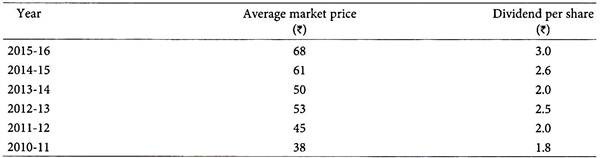
The average market prices and dividend per share of High-Tech Securities Ltd. for the past 6 years are given below:
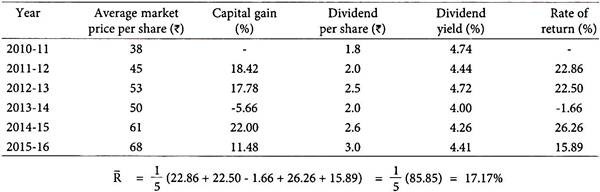
Calculate the average rate of return of High Tech Securities Ltd. Shares for past 6 years.
Solution:
Risk on Single Asset:
The concept of risk is more difficult to quantify. Statistically we can express risk in terms of standard deviation of return. For example, in case of gilt edged security or government bonds, the risk is nil since the return does not vary – it is fixed. But strictly speaking if we consider inflation and calculate real rate of return (inflation adjusted) we find that even government bonds have some amount of risk since the rate of inflation may vary.
Return from unsecured fixed deposits appear to have zero variability and hence zero risk. But there is a risk of default of interest as well as the principal. In such case the rate of return can be negative. Hence, this investment has high risk though apparently it carries zero risk. For other investments like shares, business etc., where the rate of return is not fixed, there may be a schedule of return with associated probability for each rate of return.
The mean of the probable returns gives the expected rate of return and the standard deviation or variance which is square of standard deviation measures risk. Higher the range of the probable return, higher the standard deviation and hence higher the risk. A risk averse investor will look for return where the range is low. Hence, low standard deviation means low risk.
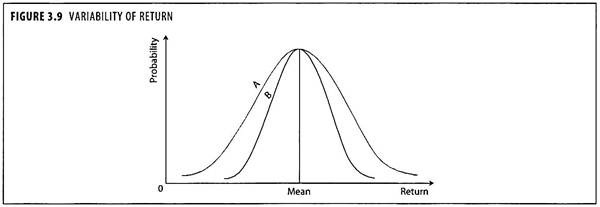
The problem in portfolio management is to minimize the standard deviation without sacrificing expected rate of return. This is possible by diversification. Risk is measured in terms of variability of returns. If Investment ‘A’ and Investment ‘B’ whose mean rate of return is same as shown in figure 3.9.
The returns of Investment ‘A’ show more variability than Investment ‘B’. In view of the variability of returns, Investment ‘A’ is more risky, even though both the investments are having the same mean returns. The following illustrations explains the quantification of risk in terms of standard deviation.
Problem 3:
The rate of return of equity shares of Karan Steels Ltd. for past six years are given below:
Calculate the average rate of return, standard deviation and variance.
Solution:
Calculation of Average Rate of Return (R̅):