Various quantitative techniques for decision making are:- 1. Mathematical Programming 2. Cost Analysis (Break-Even Analysis) 3. Cost-Benefit Analysis 4. Linear Programming 5. Capital Budgeting 6. Inventory Management 7. Expected Value 8. Decision Tree 9. Simulation 10. Queuing or Waiting Line Theory 11. Game Theory 12. Information Theory 13. Preference Theory/Utility Theory and Few Others.
Technique # 1. Mathematical Programming:
Besides the calculus, there are other management science techniques which can be employed to resolve a variety of decision problems. One such technique is Mathematical Programming which is useful whenever several factors constrain the choice of strategies. Consider the inventory problem. If the objective is simply to minimize total cost, there are no constraints which limit our choice of strategies.
If there are constraints, they might limit either the space in which inventory can be placed, the funds which can be spent on inventory, or the maximum number of orders that can be placed by the purchasing department.
This being the case, it would have become a problem in constrained minimization and mathematical programming techniques could be used to find a solution. The constraints create the environment within which decision makers strive to maximize or minimize the objectives to be achieved.
ADVERTISEMENTS:
This is the essence of mathematical programming: Constrained maximization or minimization. It becomes an intuitively appealing framework for the analysis of many types of business problems. The difficult task, however, is shouldered by the model builder, who must abstract from the environment those important elements that are to be incorporated in the mathematical model. Linear programming techniques such as Simplex method, graphical method etc., make the mathematical models to solve them.
Technique # 2. Cost Analysis (Break-Even Analysis):
Managers want to make money. The objective of the break-even analysis is to decide the optimum break-even point, that is, where profits will be highest. In making decisions, managers must pay a great deal of attention to the profit opportunities of alternative courses of action. This obviously requires that the cost implications of those alternatives are assessed. An important aspect of such cost analysis is that made between fixed and variable costs.
A cost can be classified as being fixed or variable in relation to changes in the level of activity within a given period. (In the long run, of course, all costs are variable). Fixed costs are those which remain fixed irrespective of the volume of production or sales. For example, a managing director’s salary will not vary (change) with the volume of goods produced during any year. Road tax payable for a car will not vary with its annual mileage covered. Insurance premiums, rent charges, R&D costs are a few other typical examples of fixed costs.
Variable costs vary or change in response to changes in, say, volume of production or sales or any other similar activity. Sales commissions in relation to sales levels, petrol costs in relation to miles travelled and labour, costs in relation to hours worked are obvious examples.
ADVERTISEMENTS:
Mixed costs are of hybrid nature, being partly fixed and partly variable. An example is found in telephone charges – the rental element is a fixed cost, whereas charges for calls made are a variable cost. Separating fixed and variable costs.
The total cost at any level of operations is the sum of a fixed cost component and a variable cost component. The importance of separating variable costs from fixed costs stems from the different behaviour patterns of each, which have a significant bearing on their control. Variable Costs must be controlled in relation to the level of activity, whilst fixed costs must be controlled in relation to time.
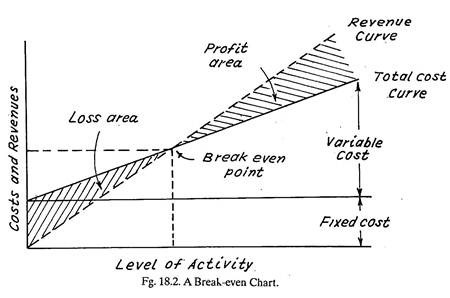
From a decision-making point of view, it is also important to know whether or not a particular cost will vary as a result of a given decision. By adding graphically variable cost to the fixed cost for different levels of activity (e.g. number of goods produced), a total cost curve can be drawn.
If a revenue curve is super-imposed on the same graph (Fig. 18.2) the result is the break-even chart which depicts the profits/loss picture for several possible cost-revenue situations at different levels of activity.
In particular, break-even analysis is useful as a background information device for reviewing overall cost and profit levels, but it can also be used in connection with special decisions such as selecting a channel of distribution or make or buy decisions.
Technique # 3. Cost-Benefit Analysis:
Cost-benefit analysis is a mathematical technique for decision-making. It is a quantitative technique used to evaluate the economic costs and the social benefits associated with a particular course of action. In this technique, an effort is made to identify all costs and benefits, not only those that may be expressed in rupees, but also the less easily calculated effects of a given decision.
In general, this technique (which is fairly complicated) is advocated for use in decisions on public projects, in which social costs and social benefits as well as actual out-of-pocket costs should be taken into account. What counts as a benefit or loss to one part of the economy—to one or more persons or groups- does not necessarily count as a benefit or loss to the economy as a whole.
And in cost-benefit analysis we are concerned with the economy as a whole, with the welfare of a defined society and not any smaller part of it. But cost-benefit analysis may also be applicable to a single company, for in many cases, it is advisable to place a value on costs and benefits that are not ordinarily expressed in rupees.
ADVERTISEMENTS:
Somewhat similar to cost-benefit analysis is the cost-effectiveness analysis, which is analysis to determine the least expensive way of reaching an objective or of obtaining the greatest possible value from a given expenditure.
Technique # 4. Linear Programming:
Linear programming is a quantitative technique used to determine the optimal mix of limited resources for maximizing profits or minimizing costs. Linear programming is an extension of break-even analysis that is very useful in analyzing complex problems. Linear programming involves the solution of linear equations and is appropriate when the manager must allocate scarce resources to competing projects.
Technique # 5. Capital Budgeting:
A manager relies heavily on linear programming when he allocates resources to competing projects. Similarly Capital budgeting provides a set of techniques a manager can use to evaluate the relative attractiveness of various projects in which a lump payment is made to generate a stream of earnings over a future period.
Examples of capita! budgeting projects include an investment in a new machine that will increase future profits by reducing costs, an investment of a sum of money into an advertising campaign to increase future sales (and profits) etc.
ADVERTISEMENTS:
In essence, capital budgeting techniques provide management with a useful method for analyzing the profitability of potential investments that have dissimilar earnings characteristics. Without these techniques, it would be nearly impossible to weigh the advantages of dissimilar investments.
Technique # 6. Inventory Management:
In quest to make money, a manager should employ his resources as efficiently as possible. Inventory management involves determining and controlling the amount of raw material an organization should keep in stock to operate effectively and efficiently.
Efficient management of inventory requires balancing several conflicting goals. The first goal is 10 Keep inventories as small as possible to minimize the amount of warehouse space and the amount of money tied up in inventories.
This goal is in conflict with the need to fill all customer requirements, to optimize the number of orders placed, and to take advantage of the economies of long production runs and quantity discounts. To solve inventory problems, the manager can use the economic order quantity (EOQ) model. This model can be expressed as a mathematical formula. The solution of EOQ formula tells the manager how many items he should purchase, and how often.
Technique # 7. Expected Value:
ADVERTISEMENTS:
To understand expected value model, it is important to comprehend the concept of probability which refers to the likelihood that an event will happen. Mathematically, probability is expressed as a fraction or percentage.
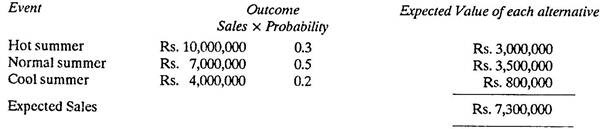
For example, there is a 30% (or 0.3) probability that it will rain tomorrow. Probabilities may be established empirically, by observing some phenomenon over time. When several courses of action are available and the outcome of each is uncertain, the decision maker can use probabilities to select his final choice.
Taking an example:
The sales of an air-conditioner will depend on how hot the summer is. The expected value for any event is the income it would produce times its probability. Adding the expected values of all possible events, yields expected sales, the average level of sales that can be expected over the long run if the given probabilities hold, as shown in table below. For the air-conditioner, expected sales for the summer are Rs. 7,300,000.
Technique # 8. Decision Tree:
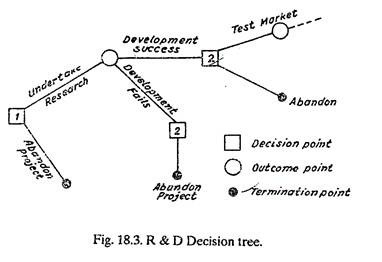
Another increasingly useful tool for management decision-makers is the so called decision tree. This is basically a conceptual map of possible decisions and outcomes in a particular situation. It is useful in cases where a manager is required to make a number of sequential decisions i.e., where earlier decisions will affect later ones.
A simple decision tree appears below:
The above diagram focuses attention on outcomes or consequences as well as decisions. These outcomes can be further elaborated in terms of their probability and their anticipated pay off. It is also possible to add a time dimension to the whole diagram, so that, for example in Fig. 18.3 the period from decision point 1 to decision point 2 could be one year. These additional features help to make the use of decision trees a salutary exercise for managers.
Technique # 9. Simulation:
Simulation techniques are especially applicable to what if problems, in which a manager or technician wants to know, If we do this, what will happen. Simulation can, of course, be conducted by the manipulation of physical models. For example, one might have a physical model of a machine and actually keep on increasing its speed to determine at what point it would begin to jam, fly apart or walk across the floor.
With no loss, one may, instead, use a mathematical model in which each of the terms represents one of the variables, and observe the effect on the others when different values are given to one or more of the terms. With the help of a computer, it is possible to examine what will happen in an enormous number of cases-without spending a prohibitive amount of time.
ADVERTISEMENTS:
Because large electronic computers have become easily accessible in recent years, management can simulate complex situations in order to determine the best course of action. Simulation is the process of building, testing and operating models of real-world phenomena through the use of mathematical relationships that exist among critical factors.
This technique is useful for solving complex problems that cannot be readily solved by other techniques. A simulation model can be deterministic if the manager knows exactly the value of the factors he employs in the equations.
However, simulation is essentially probabilistic, since the manager typically must estimate the future values of these factors. Simulation is very helpful in engineering and design problems, where the medium may be either the mathematical model or a diagram on a screen (VDU) connected to the computer. In the latter case, the engineer-designer can modify the design by using a light pen. The technique is equally applicable to management decision-making.
It is obviously much cheaper, safer and easier to experiment with a mathematical model or diagrammatic simulator than to experiment with real machines or even physical models of machines. In some cases, however the variables that one manipulates are not exact quantities but probabilities. Then what are known as Monte Carlo techniques must be used. These make it possible to stretch as far as possible such few actual data as are available to begin with.
Technique # 10. Queuing or Waiting Line Theory:
Queuing theory is an O.R. technique which aids the manager in making decisions involving the establishment of service facilities to meet irregular demands. Cost problems arise when there are more service facilities available than are needed, or when too few facilities are available and consequently, long waiting lines form.
For example, in a battery of machines, breakdowns will occur randomly, and whenever the maintenance service falls below that demanded by the breakdowns, a waiting line of unrepaired machines forms. This idle capacity is a cost that has to be balanced against the costs of keeping maintenance services available.
ADVERTISEMENTS:
Queuing theory is applied to any situation producing a need to balance the cost of increasing available service against the cost of letting units wait. To arrive at the best number of service facilities, the manager and the O.R. team must first determine (in the example above) the breakdown rate and the time required to service each machine.
These data can then be used to construct a mathematical model of the problem, which can become extremely complex. Simulation methods are widely used to solve waiting line problems. Simulation is a systematic, trial and error procedure for solving waiting line & problems that are too complex for easy mathematical analysis.
Reasonably good solutions may often be obtained by simulating important elements of the problem. A widely used method of simulating business problems in which events occur with assigned or computed probabilities is known as the Monte Carlo Method. This method utilizes the mathematics of probability, and is often run on the computer.
Technique # 11. Game Theory:
Game theory is a technique of operations research. This provides a basis for determining, under specified conditions, the particular strategy that will result in maximum gain or minimum loss, no matter what opponents do or do not do. (An opponent would be the enemy general in military application, or a competitor in a business situation etc.)
The simplest application of the game theory is the two-person, zero-sum game, in which there are only two players and one player can gain only at the expense of the other. These two conditions are generally fulfilled when two armies are opposing each other. In business they are fulfilled only in special cases.
Assume, a company has only one competitor and the size of the market is fixed; thus every gain in sales by one company means an equal loss in sales for the other. In an expanding market, both the companies could gain, in a declining market, one could gain at the expense of the other. Game theory has the greatest practical usefulness in planning sales promotion strategies.
ADVERTISEMENTS:
A Company who wishes to increase its sales may do so by using one or more of such techniques as:
(1) A reduction in product price,
(2) An increase in number of salesmen, and
(3) A rise in its advertising budget,
The company must consider what the rival can do to nullify the effect of any of these techniques. The company therefore asks itself questions like these.
Assuming we decide to increase our share of market by cutting prices, what will actually happen if:
ADVERTISEMENTS:
(a) Our rival also cuts prices,
(b) He increases the number of his salesmen,
(c) He raises his advertising budget or
(d) He uses a combination of all three of these tactics?
By evaluating each one of these possibilities, the company can ascertain the greatest possible damage the rival can inflict. This will reveal either the minimum gain the company is assured of or the maximum loss it can suffer.
In real life, however, there are more than two competitors and the demand for most products is not stable or fixed. If all competitors cut prices, the market for all may be increased and possibly all may gain. Or, if the market remains the same, all may lose. Therefore the losses of one do not necessarily equal the gains of another.
ADVERTISEMENTS:
Game Models:
The next quantitative decision making model consists of game models or competitive strategies. These models are derived from game theory which provides many useful insights into situations involving elements of competition.
Decision situations are of a game nature when a rational opponent (e.g., a competitor in the market) is involved, so that resulting effects are dependent on the specific strategies selected by the decision maker and his opponent. This assumes that the opponent will carefully consider what the decision maker may do before he selects his own strategy.
Technique # 12. Information Theory:
A central element in all decision making is the process of obtaining, using and disseminating information. Information theory is a rigorous mathematical effort to solve problems in communication engineering. Since information theory deals with the flow of information and communication net-works, it has important implications for organization design and for man-machine relationships.
Information theory provides a means of measuring the information content of both symbolic and verbal languages and relating the characteristics of an efficient communication system to the information content of messages transmitted. This body of theory has been of great use in the design of communication systems and computers.
Technique # 13. Preference Theory/Utility Theory:
One of the interesting and practical supplements of modern decision theory is (the work that has been done and) the techniques developed to supplement statistical probabilities with analysis of individual preferences in the assumption or avoidance of risk. While referred to here as preference theory, it is more classically denoted Utility theory. It might seem reasonable that if we had a 60% chance of a decision being the right one, we would take it.
But this is not necessarily true, since the risk of being wrong is 40% and a manager might not wish to take this risk, particularly if the penalty for being wrong is severe, whether in terms of monetary losses, reputation or job security. If we doubt this, we might ask ourselves whether we would risk, say Rs. 40,000 on the 60% chance that we might make Rs. 100,000.
We might readily risk Rs. 4 on a chance of making Rs. 10, and gamblers have been known to risk much more on a lesser chance of success. Therefore, in order to give probabilities practical meaning in decision making, we need better understanding of the individual decision maker’s aversion to, or acceptance of risk. This varies not only with people but also with the size of the risk, with the level of managers in an organization and according to whether the funds involved are personal or belong to a company.
Higher level managers are accustomed to taking larger risks than lower-level managers. The same top manager who may take a decision involving risks of millions of rupees for a company would not like to do that with his own personal fortune. Moreover, the same manager willing to opt for a 75% risk in one case might not be willing to, in another.
For example, he may go for a large advertising program where the chances of success are 70%, but might not decide in favour of an investment in plant and machinery unless the probabilities for success were higher. In other words, attitudes toward risk vary with events, as well as with people and positions.
Most of us are gamblers when small stakes are involved, but soon take on the role of risk averters when the stakes rise. Many managers are risk averters and thereby miss opportunities.
Technique # 14. Heuristic Programming:
Heuristic programming, sometimes called heuristic problem solving, is an approach to decision making that has gained increasingly wide usage in recent years. It is in fact a branch of simulation model analysis. It is applied to problems in such areas as assembly line balancing, plant layout, job shop scheduling, warehouse location and resource allocation. A heuristic is any device or procedure used to reduce problem-solving effort. A rule-of-thumb is a commonly used heuristic.
For example, the rule that “when there are only ten parts in the bin, reorder the part” or “do not drink liquor and drive a car”, are examples of heuristics. Much business behaviour and much in everyday life is guided by this kind of rule. When heuristics are combined to solve a problem, a heuristic program is formed. Complex programs require computers for their solution. Heuristic programs are used wherever the problem is too large or too complex to solve by mathematical or statistical techniques.
It is also used to deal with ill-structured problems that cannot be stated in mathematical terms, so that quantitative techniques (such as O.R.) are not suitable for such problems. The chief inputs in heuristic programming are subjective, based on the managers past experience, the pooling of knowledge and judgments of colleagues, the use of judgment, intuition, creativity, learning processes and other qualitative variables.
The decision maker immerses himself in the total problem, and searches by means of trial and error for a satisfactory solution in a reasonable time and at a reasonable cost, rather than striving for an optimal solution at all costs.
Technique # 15. Decision Theory:
Decision Theory may be defined as a set of general concepts and techniques that assist a decision maker in choosing among alternatives.
Decision theory problems are commonly cast in a standard framework, termed a decision matrix which consists of the following components:
(a) Strategies or alternatives (S), available to the decision maker. For example make and buy would be two strategies in a make-or-buy decision problem. Strategies are within the control of the decision maker.
(b) States of nature (N), which are characteristics of the environment and are beyond the control of the decision maker. The term derives from the Weather, where we might observe, say, three states of nature: sunshine, rain or snow.
In business decisions, states of nature might be various levels of demand for a product, the number of competitors, governmental actions etc.
(c) Predictions of likelihood (Pr) or the probability associated with the occurrence of each state of nature. If a particular state of nature is sure to occur (Pr = 1.0), the decision situation is termed one of certainty.
If the decision maker can assign probability of occurrence to one or more states of nature, with no one state given a value of 1.0, it is termed a risk situation.
Finally, if the decision maker has no idea of the probabilities of occurrence of any state of nature, the situation is defined as decision making under uncertainty.
Thus in the decision matrix above, there would be an entry for probability if the situation is one of certainty or risk and no entry if it is one of uncertainty.
(d) Pay offs or outcomes (O), which represent the value associated with each combination of strategy and state of nature. The value may be stated in terms of utility, cost, profit, satisfaction etc.
Solving a decision theory problem obviously requires some choice to be made from among the alternatives, and thus some rule or decision criterion must be selected for this purpose. For example, in certainty situations, the decision criterion is to select the single strategy with the highest pay off. Since only one state of nature is relevant, this entails a simple scanning of the payoff column under the certain N and picking the best one.
Technique # 16. Cost Effectiveness Analysis:
Cost effectiveness analysis is a decision making methodology that ultimately leads to a comparison of alternatives in terms of their costs and effectiveness in attaining some specific objective.
It differs from conventional economic analysis in that it attempts to devise a quantitative criterion that can simultaneously measure both the quantitative and qualitative elements of a decision problem.
Because its methodology permits analysis of alternatives with widely ranging physical and operational characteristics, it has been applied in situations where a general objective can be achieved in many ways.
In addition to industrial applications, cost-effectiveness analysis has been applied to problems of:
i. Health care: Urban planning
ii. Law enforcement: Defense etc.
The procedure for performing a cost effectiveness analysis typically includes the following steps:
(1) Define objectives that the systems are to fulfill. For example, objective may be to produce a high- quality newspaper in sufficient quantity to meet daily demand for the next 10 years.
(2) Identify mission requirements essential to the attainment of the objectives. There are the individual system’s goals, which must be met if the overall objective is to be achieved. In this example they are: Meet a specified demand (of say 100,000 newspapers a day) and print parts of the paper in atleast five colours.
(3) Develop alternative systems for accomplishing the system.
(4) Establish basis for evaluating alternative systems.
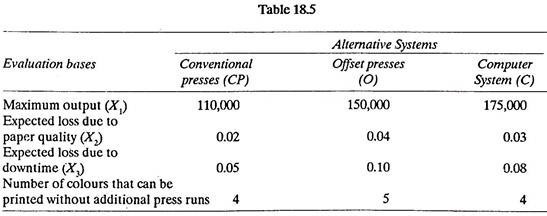
Steps (3) and (4) are shown in Table 18.5.
(5) Formulate Effectiveness Model:
Evaluation basis variables X1, X2, X3 can be converted to a single measure, E.
E = Salable papers/day = (X1) (1 – X2) (1 – X3)
Effectiveness of CP = (110,000) (1 – 0.02) (1 – 0.05) = 102,410
Effectiveness of O = (150,000) (1 – 0.04) (1 – 0.10) = 129,600
Effectiveness of C = (175,000) (1 – 0.03) (1 – 0.08) = 156,170
(6) Formulate Cost Model:
The cost function should reflect the present value of all associated costs for each alternative, discounted over a 10 year time horizon.
The function would be:
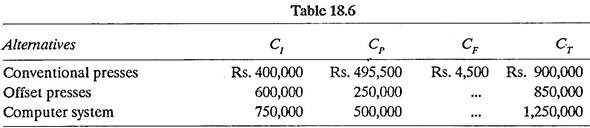
CT = CI + CP + CF where
CT = Grand total cost for a proposed plan of action.
CI = Total cost incurred for initial investment.
CP = Total cost incurred for production operations over a 10 years’ time horizon.
CF = Cost of additional desirable feature(s), for example, colour reproduction capability.
The costs CP and CF are new data inputs and CI came from the decision theory problem. These are used to derive CT (refer table 18.6).
(7) Select Decision Criterion:
Several different decision criteria have been employed to rank and select alternatives:
(a) Maximize effectiveness divided by cost (max. E ÷ C)
(b) Maximize effectiveness minus cost (max. E – C)
(c) Maximize effectiveness given a fixed cost (max. E/C)
(d) Minimize cost given a fixed effectiveness (min. C/E)
For this example we will choose number (a), although each has its pros and cons.
(8) Analyze Systems Costs Versus Effectiveness:
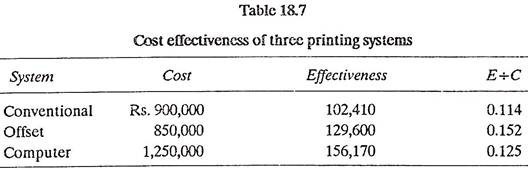
Table 18.7 represents the cost, effectiveness value and the£+C ratio for each candidate system.
On the basis of the effectiveness ratio criterion, the choice would be the offset press. However, before finalizing the decision, the management should also consider the importance of those factors which could not be quantified – for example, management skill in handling several technologies, operator availability and the training required for each alternative, proven capability of each process in other situations etc.
(9) Perform Sensitivity Analysis:
In many cost-effectiveness studies, the decision is very sensitive to the assumptions. In this example, it was assumed that demand would be atleast 100,000 papers per day; however, if demand reaches 120,000 papers per day, the conventional press system under consideration would be inadequate. Thus a sensitivity analysis might also be made using a variety of conventional press systems.
Finally, the offset press system requires a better quality paper than the conventional press and in many locales such paper is provided by only a few suppliers. Thus if there is a problem with a supplier, the expected loss due to paper quality might be much higher than the assumed 4% because of having to use a lower-quality paper or having to wait for shipment from a more distant source.