Different methods employed for comparing alternative investments and to ascertain the profitability of each project are:- 1. Pay-back method. 2. Return on investment method. 3. Present-value return on investment method. 4. Return on total capital employed. 5. Linear programming model. 6. Simulation technique.
1. Pay-Back Method:
The method attempts to determine the number of years in which the investment is expected to pay for itself. For example, if a machine is to cost Rs. 100,000 and extra revenue is expected to amount to Rs. 20,000 the first year, Rs. 40,000 the second year and Rs. 40,000 in the third year, then the pay-back period is three years. In practice, these calculations may not be so simple. A fixed asset cannot usually be treated as a separate entity.
The introduction of a new machine often introduces problems. It may displace an older machine. There may be a rearrangement of duties between workers. Quite likely some costs may be reduced. Therefore, both the costs incurred and the costs saved will have to be taken into account. When comparing different alternatives, the one which pays for itself first is the one selected. The pay-back method has the advantage that it is simple to understand and operate.
Furthermore it shows how quickly the investment will be recovered. Although this method has many followers, it also has many critics. Some accountants have rightly pointed out that the true profitability of investments cannot be determined merely by considering the pay-back period.
Indeed, in that period only the recovery of costs is considered. The profit comes after all costs have been recovered and not before. Therefore, much better results would be obtained by considering the full serviceable life of each asset: only then can the total, expected profit be ascertained.
2. Return on Investment Method:
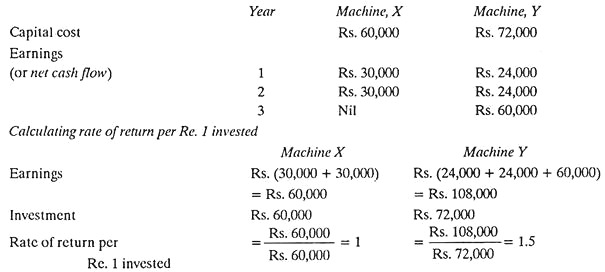
This method considers the rate of return to be obtained from the investment. When comparing alternative courses of action, the investment which shows the highest return is the one normally selected. The rate of return may be expressed as a percentage of the average amount. A simple method of obtaining the average amount is to divide the total investment by two.
c. The following illustration will explain how to calculate rate of return:
This shows the superiority of machine y over X.
The weakness of this method is—the same results would have been shown even if the full earnings of machine Y that is Rs. 108,000 would have been only in the third year. In other words, this method ignores the timing of the receipts, whereas money received earlier is more valuable.
3. Present-Value Return on Investment Method:
A serious limitation of the pay-back method was the time factor. Sums of money received at different times in the future have to be discounted to present value. Otherwise no true comparison of different investments can be made.
The present-value return method, discussed below, overcomes this obvious weakness of the payback method. A person faced with the choice of having Rs. 100 now or after one year, normally like to have it now.
If he was offered Rs. 100 now, but Rs. 110 after one year then he may be tempted to wait for Rs. 110. This simple example illustrates the present value concept of money. As above, if 10% is taken to be a normal rate of return for a particular type of investment, the Rs. 100 due in one year is at present worth only Rs. 90.91.
If it is necessary to wait two years for Rs. 100, then taking compound interest at 10%, the present value is Rs. 82.64. The object of all the methods being described is to arrive at the most profitable investment. The present-value return method is no exception. When this method is used, there are two ways of tackling the problem of calculating profitability.
These may be summarised as follows:
(i) Trial and Error Yield Method, Procedure of:
(a) List the annual sales and costs (other than depreciation) and deducting the latter from the former, obtain the net cash flow (or earnings).
(b) Obtain the capital cost. Often this will already be at present value because the cash is spent now.
(c) Calculate the present value of the net cash flow by using an appropriate rate of interest. This rate is found by trial and error from present value tables. The object is to make the cash flow equal to the capital cost.
(d) Carryout this procedure for each project being considered and then rank the projects in order of preference.
(ii) Net Gain Method:
The net gain method attempts to arrive at the difference between the present value of receipts and payments. As with previous method, the cash flows should be taken. One of the difficulties of this method is the selection of an appropriate rate of interest. One rate will give different results from another. The principal object should be to assess a return which reflects what can be expected from putting the money in alternative investments.
4. Return on Total Capital Employed:
This method approaches the problem by ensuring that the total capital employed earns an adequate return. Additional assets purchased should increase, or at least keep constant, the percentage rate of return on total capital employed.
5. Linear Programming Model:
When the firm must consider several alternatives, each of which requires cash outflows over many periods, the use of a linear programming model can be an effective way of generating a feasible investment mix.
In fact this method can be employed whenever factors such as capital, labor and equipment constrain the investment choice. In a large firm, with many investment proposals being generated each year, it is not hard to imagine how such a linear programming model could get exceedingly large.
6. Simulation Technique:
It was assumed that the data required for the discounted cash flow and linear programming methods was known with certainty. This, however, is rarely true. A more general approach to the analysis of investments requires the introduction of the concept of risk.
The distinguishing feature of models which incorporate this aspect is that they take into account the full range of possible outcomes for each factor rather than just its expected value. Since models of this sort generally become quite complex, simulation techniques must be employed. It is also easy to see how these simulation models might become quite large.
As we introduce more and more variables, the necessity for using a computer becomes apparent. Building a large-scale simulation model is not very difficult; what difficult is, justifying the fact that the incremental benefit associated with a more complex model is greater than the incremental cost.